| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- augmentedDevice
- react-native-dotenv
- adb pair
- nextjs
- animation
- html
- react-native
- dvh
- github lfs
- silent printing
- Can't resolve
- vercel git lfs
- custom printing
- npm package
- Git
- camera access
- ELECTRON
- ffi-napi
- 티스토리 성능
- device in use
- rolldown
- Each child in a list should have a unique "key" prop.
- camera permission
- Recoil
- github 100mb
- Failed to compiled
- github pdf
- adb connect
- 이미지 데이터 타입
- electron-packager
- Today
- Total
Bleeding edge
[프로그래머스] 멀쩡한 사각형 - 자바스크립트 0606 본문
문제 설명
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.
제한 사항
- W, H : 1억 이하의 자연수
https://programmers.co.kr/learn/courses/30/lessons/62048
코딩테스트 연습 - 멀쩡한 사각형
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을
programmers.co.kr
문제 풀이가 어려운 문제는 아니고 이 문제에 왜 최대공약수가 사용되는지를 고민하는게 어려웠었던 문제였다.
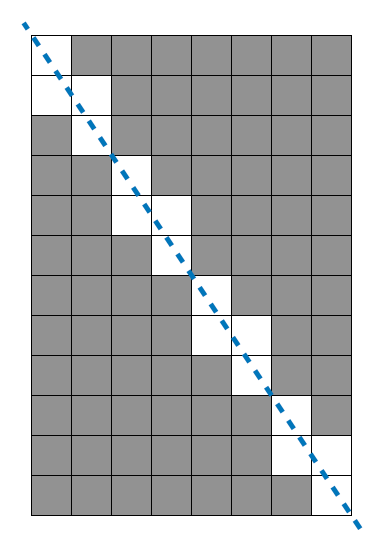
이문제의 변수는 w와 h로 주어지며 정사각형의 갯수의 높이와 너비를 각각 의미한다. 이 문제의 정답을 구하기 위해서는 더해야할 것과 빼야할 것들을 구해야한다
전체 사각형 갯수 - 0,0부터 w,h까지 선을 그리면 생기는 사각형의 갯수
전체 사각형의 갯수같은 경우 w*h이기 때문에 간단하다.
하지만, 선을 그리면서 생기는 사각형의 갯수같은 경우에는, 테스트케이스에서 그려진 경우인 12, 8을 조금더 쪼개서 6,4 더쪼개서 3, 2를 보면 선을 그릴때 모양이 12, 8과 유사하다는 것을 볼 수 있다. 이 그려지는 사각형은 w, h의 최대약수를 이용한다는 것을 알 수 있다. 그리고 이 선이 6, 4로 늘어났을 때 그리고 12, 8을 계산해보면 w+h - 최대공약수(w,h의) 라는 것을 구할 수 있다. 따라서 최대공약수를 구하는 함수를 solution에 넣었다.
const gcd = (a,b) => a%b===0? b : gcd(b, a%b)그리고 이 문제에서는 gcd 를 제외하고는, 특이한 식이 필요하지 않기 때문에 return에 식을 정리해서 넣었다
function solution(w, h) {
const gcd = (a,b) => a%b===0? b : gcd(b,a%b)
return w*h-(w+h-gcd(w,h))
}문제 자체가 어렵진 않지만 규칙을 파악하는데 시간이 많이 걸렸다. 규칙이 보이는 문제 같은경우 손으로 푸는 습관을 더 가져야할꺼같다.
'코딩테스트 공부' 카테고리의 다른 글
| [leetcode] 28. Implement strStr() - 자바스크립트 0607 (0) | 2022.06.07 |
|---|---|
| [leetcode] 14. Longest Common Prefix - 자바스크립트 0607 (0) | 2022.06.07 |
| [프로그래머스] 직사각형 별찍기 - 자바스크립트 0606 (0) | 2022.06.06 |
| [프로그래머스] 2 x n 타일링 -자바스크립트 (0) | 2022.06.02 |
| [프로그래머스] 가장 큰 정사각형 - 자바스크립트 (0) | 2022.05.30 |
